Seismic vulnerability assessment of urban environments in moderate-to-low seismic hazard regions using association rule learning and support vector machine methods

Abstract

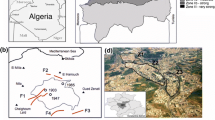
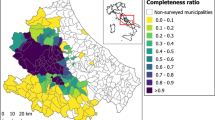
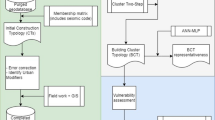
The estimation of the seismic vulnerability of buildings at an urban scale, a crucial element in any risk assessment, is an expensive, time-consuming, and complicated task, especially in moderate-to-low seismic hazard regions, where the mobilization of resources for the seismic evaluation is reduced, even if the hazard is not negligible. In this paper, we propose a way to perform a quick estimation using convenient, reliable building data that are readily available regionally instead of the information usually required by traditional methods. Using a dataset of existing buildings in Grenoble (France) with an EMS98 vulnerability classification and by means of two different data mining techniques—association rule learning and support vector machine—we developed seismic vulnerability proxies. These were applied to the whole France using basic information from national databases (census information) and data derived from the processing of satellite images and aerial photographs to produce a nationwide vulnerability map. This macroscale method to assess vulnerability is easily applicable in case of a paucity of information regarding the structural characteristics and constructional details of the building stock. The approach was validated with data acquired for the city of Nice, by comparison with the RiskUE method. Finally, damage estimations were compared with historic earthquakes that caused moderate-to-strong damage in France. We show that due to the evolution of vulnerability in cities, the number of seriously damaged buildings can be expected to double or triple if these historic earthquakes were to occur today.

Appendix

1.1 Support vector machine definitions (SVM)

For the sake of simplicity, a formal definition of the linear binary case is first presented. The nonlinear case (still binary) is then studied. At last, the multiclass case is considered (n-class classification problem). Definitions are built following Teukolsky et al. (2007) and Cortes and Vapnik (1995).

1.2 Linear classification

Before entering into the mathematical definitions, a qualitative graphical description will help understanding the basic foundation of the method. Given some data points belonging to one of two classes (binary problem), viewed as p-dimensional vectors (a list of p numbers) for SVM, many planes might exist that classify the data (Fig. 17). Intuitively, a good separation is achieved by the plane that has the largest distance to the nearest training data point of any class (so-called functional margin), since in general the larger the margin is, the lower the generalization error of the classifier. Therefore, the basic idea is to choose the plane so that the distance from it to the nearest data point on each side is maximized.

Fig. 17

Different separating hyperplanes. A does not separate the classes. B does, but only with a small margin. C separates them with the maximum margin

Given some training data $D$, a set of points of the form

$$ D = \{ (\varvec{x}_{i } ,y_{i} )|\varvec{x}_{i } \in {\mathbb{R}}^{p} , \quad y_{i} \in \left\{ { - 1, 1} \right\}\}_{i = 1}^{n} $$

where the $y_{i}$ is either 1 or −1, indicating the class to which the point $\varvec{x}_{i}$ belongs. Each $\varvec{x}_{i}$ is a p-dimensional real vector. We want to find the maximum-margin hyperplane that divides the points having $y_{i } = 1$ from those having $y_{i} = - 1$. Any hyperplane can be written as the set of points $\varvec{x}$ satisfying

$$ \varvec{w} \cdot \varvec{x} + b = 0 $$

where · denotes the dot product and $\varvec{w}$ the normal vector to the hyperplane. The parameter $\frac{b}{{\left\| \varvec{w} \right\|}}$ determines the offset of the hyperplane from the origin along the normal vector $\varvec{w}$ (Fig. 18). If the training data are linearly separable, we can select two hyperplanes in a way that they separate the data and there are no points between them, and then try to maximize their distance. The region bounded by them is called “the margin.” These hyperplanes can be described by the equations (see Fig. 18)

Fig. 18

Maximum-margin hyperplane and margins for an SVM after training with samples from two classes. Samples on the margin are called the support vectors

$$ \varvec{w} \cdot \varvec{x} + b = 1\;{\text{and}}\;\varvec{w} \cdot \varvec{x} + b = - 1 $$

By using geometry, we find the distance between these two hyperplanes is $\frac{2}{{\left\| \varvec{w} \right\|}}$, so we need to minimize $\left\| \varvec{w} \right\|$. As we also have to prevent data points from falling into the margin, we add the following constraint: for each $i$ either

$$ \begin{gathered} \varvec{w} \cdot \varvec{x}_{i } + b \ge 1\quad {\text{for}}\;\varvec{x}_{i} \;{\text{of}}\;{\text{the}}\;{\text{first}}\;{\text{class}},\;{\text{or}} \hfill \\ \varvec{w} \cdot \varvec{x}_{i } + b \le - 1\quad {\text{for}}\;\varvec{x}_{i} \;{\text{of}}\;{\text{the}}\;{\text{second}}\;{\text{class}} \hfill \\ \end{gathered} $$

This can be rewritten as

$$ y_{\varvec{i}} \varvec{ }(\varvec{w} \cdot \varvec{x}_{i } + b) \ge 1\quad {\text{for}}\;{\text{all}}\;1 \le i \le n $$

The optimization problem is then posed as:

$$ {\text{Minimize(in}}\,\varvec{w},b )\left\| \varvec{w} \right\|;\quad {\text{subjected}}\;{\text{to}}\; ( {\text{for any}}\;i = 1, \ldots ,n)\,y_{i} (\varvec{w} \cdot \varvec{x}_{i} ) \ge 1 $$

To simplify the problem, it is possible to alter the equation by substituting $\left\| \varvec{w} \right\|$, the norm of w, with $\frac{1}{2}\left\| \varvec{w} \right\|^{2}$ without changing the solution (the minimum of the original and the modified equation has the same $w$ and $b$). This is a quadratic programming optimization problem.

$$ {\text{Minimize(in}}\,\varvec{w},b )\frac{1}{2}\left\| \varvec{w} \right\|^{2} ;\quad {\text{subjected}}\;{\text{to}}\; ( {\text{for any}}\;i = 1, \ldots ,n)\,y_{i} (\varvec{w} \cdot \varvec{x}_{i} ) \ge 1 $$

In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints.

By introducing Lagrange multipliers $\varvec{\alpha}$, the previous constrained problem can be expressed as

$$ \mathop {\hbox{min} }\limits_{{\varvec{w}, b}} \mathop {\hbox{max} }\limits_{\alpha \ge 0} \left\{ {\frac{1}{2}\left\| \varvec{w} \right\|^{2} - \mathop \sum \limits_{i = 1}^{n} \alpha_{i} [y_{i } \left( {\varvec{w} \cdot \varvec{x}_{i} + b} \right) - 1]} \right\} $$

This problem can now be solved by standard quadratic programming techniques and programs. The “stationary” Karush–Kuhn–Tucker condition implies that the solution can be expressed as a linear combination of the training vectors

$$ \varvec{w} = \mathop \sum \limits_{i = 1}^{n} \alpha_{i} y_{i} \varvec{x}_{i} $$

Only a few $\alpha_{i}$ will be greater than zero. The corresponding $\varvec{x}_{i}$ is exactly the support vector that lies on the margin and satisfies

$$ y_{\varvec{i}} \varvec{ }\left( {\varvec{w} \cdot \varvec{x}_{i } + b} \right) = 1 $$

From this, we can derive that the support vectors also satisfy

$$ \varvec{w} \cdot \varvec{x}_{i} + b = \frac{1}{{y_{i} }} = y_{i} \Leftrightarrow b = \varvec{w} \cdot \varvec{x}_{i} - y_{i} $$

which allows defining the offset $b$. In practice, it is more robust to average over all support vectors $N_{\text{sv}}$

$$ b = \frac{1}{{N_{\text{sv}} }} \mathop \sum \limits_{i = 1}^{{N_{\text{sv}} }} (\varvec{w} \cdot \varvec{x}_{i} - y_{i} ) $$

A modified maximum-margin idea was proposed, allowing for mislabelled examples. If there exists no hyperplane that can split the examples (some points may fall within the margins), the Soft Margin method will choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearest cleanly split examples. The method introduces slack variables $\zeta_{i}$, which measure the degree of misclassification of the data $x_{i}$.

$$ y_{\varvec{i}} \varvec{ }\left( {\varvec{w} \cdot \varvec{x}_{i } + b} \right) \ge 1 - \zeta_{i} \quad 1 \le i \le n $$

The optimization becomes a trade-off between a large margin and a small error penalty. The final equation leads to a quadratic programming solution. The membership decision rule is based on the sign function, and the classification is done by $y_{\text{new}} = \text{sgn} \left( {\varvec{w} \cdot \varvec{x}_{\text{new}} + b} \right)$ where $(\varvec{w}, b)$ are the hyperplane parameters found during the training process, and $x_{\text{new}}$ is an unseen sample.

1.3 Nonlinear classification

In addition to performing linear classification, SVMs can efficiently perform nonlinear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces. For machine learning algorithms, the kernel trick is a way of mapping observations from a general set S into an inner product space V, in the hope that the observations will gain meaningful linear structure in V. Linear classifications in V are equivalent to generic classifications in S. The trick to avoid the explicit mapping is to use learning algorithms that only require dot products between the vectors in V, and choose the mapping such that these high-dimensional dot products can be computed within the original space, by means of a kernel function. The resulting algorithm is formally similar, and the maximum-margin hyperplane can be fitted in the transformed feature space. The transformation may be nonlinear, and the transformed space was high dimensional; therefore, even if the classifier is a hyperplane in the high-dimensional feature space, it may be nonlinear in the original input space (Fig. 19). There exist several choices of kernel function $k$. The Kernel is related to the transform $\phi (x_{i} )$ by the equation $k(\varvec{x}_{i} ,\varvec{x}_{j} ) = \phi (x_{i} ) \cdot \phi (x_{j} )$.

Fig. 19

Kernel machine. The separation surface can become linear when feature vectors are mapped in a high-dimensional space (here 3D—right) while it may be nonlinear in the original input space (here 2D—left)

Generally, the Gaussian kernel is a common good choice $k(\varvec{x}_{i} ,\varvec{x}_{j} ) = \exp \left( { - \frac{1}{2} |\varvec{x}_{i} - \varvec{x}_{j} |^{2} /\sigma^{2} } \right)$, and it proved to give the best results in our study. Therefore, the classifications in this work are done using this kernel.

1.4 Multiclass SVM

Even if SVM are intrinsically binary classifiers, in practice several-classes classifications are usually of interest. Different multiclass classification strategies can be adopted, based on the binary analysis or the less used “all-together” method. The former is the dominant approach, which reduces the single multiclass problem into multiple binary classification problems and can be of the form (among others):

1.4.1 One versus all

Involves training N different binary classifiers, each one trained to distinguish the data in a single class from the data in all remaining classes. Classification of new instances is done by a winner-takes-all strategy, in which the classifier with the highest output function assigns the class.

1.4.2 One versus one

Builds binary classifiers that distinguish between every pair of classes. Classification is done by a max-wins voting strategy, in which every classifier assigns the instance to one of the two classes, then the vote for the assigned class is increased by one vote, and finally, the class with the most votes determines the instance classification. The one-versus-one classification proved to be more robust in the majority of cases, and showing the best results is the one selected in our study.